 |
JKQTPlotter trunk/v5.0.0
an extensive Qt5+Qt6 Plotter framework (including a feature-richt plotter widget, a speed-optimized, but limited variant and a LaTeX equation renderer!), written fully in C/C++ and without external dependencies
|
 |
JKQTPlotter trunk/v5.0.0
an extensive Qt5+Qt6 Plotter framework (including a feature-richt plotter widget, a speed-optimized, but limited variant and a LaTeX equation renderer!), written fully in C/C++ and without external dependencies
|
Enumerations | |
| enum class | JKQTPStatRegressionModelType { JKQTPStatRegressionModelType::Linear , JKQTPStatRegressionModelType::PowerLaw , JKQTPStatRegressionModelType::Exponential , JKQTPStatRegressionModelType::Logarithm } |
| when performing linear regression, different target functions can be fitted, if the input data is transformed accordingly. This library provides the options in this enum by default. More... | |
Functions | |
| template<class InputItX, class InputItY> | |
| double | jkqtpstatCoefficientOfDetermination (InputItX firstX, InputItX lastX, InputItY firstY, InputItY lastY, std::function< double(double)> f) |
| calculates the coefficient of determination | |
| jkqtmath_LIB_EXPORT std::pair< std::function< double(double)>, std::function< double(double)> > | jkqtpStatGenerateParameterATransformation (JKQTPStatRegressionModelType type) |
Generates the transformation function for a-parameter (offset, result.first : transform, result.second : back-transform) for each regression model in JKQTPStatRegressionModelType in type. | |
| jkqtmath_LIB_EXPORT std::pair< std::function< double(double)>, std::function< double(double)> > | jkqtpStatGenerateParameterBTransformation (JKQTPStatRegressionModelType type) |
Generates the transformation function for b-parameter (slope, result.first : transform, result.second : back-transform) for each regression model in JKQTPStatRegressionModelType in type. | |
| jkqtmath_LIB_EXPORT std::function< double(double, double, double)> | jkqtpStatGenerateRegressionModel (JKQTPStatRegressionModelType type) |
Generates functors f(x,a,b) for the models from JKQTPStatRegressionModelType in type. | |
| jkqtmath_LIB_EXPORT std::function< double(double)> | jkqtpStatGenerateRegressionModel (JKQTPStatRegressionModelType type, double a, double b) |
Generates functors f(x) for the models from JKQTPStatRegressionModelType in type and binds the parameter values and b to the returned function. | |
| jkqtmath_LIB_EXPORT std::pair< std::function< double(double)>, std::function< double(double)> > | jkqtpStatGenerateTransformation (JKQTPStatRegressionModelType type) |
Generates the transformation function for x-data (result.first ) and y-data (result.second ) for each regression model in JKQTPStatRegressionModelType in type. | |
| template<class InputItX, class InputItY> | |
| void | jkqtpstatLinearRegression (InputItX firstX, InputItX lastX, InputItY firstY, InputItY lastY, double &coeffA, double &coeffB, bool fixA=false, bool fixB=false) |
| calculate the linear regression coefficients for a given data range firstX / firstY ... lastX / lastY where the model is | |
| template<class InputItX, class InputItY, class InputItW> | |
| void | jkqtpstatLinearWeightedRegression (InputItX firstX, InputItX lastX, InputItY firstY, InputItY lastY, InputItW firstW, InputItW lastW, double &coeffA, double &coeffB, bool fixA=false, bool fixB=false, std::function< double(double)> fWeightDataToWi=&jkqtp_identity< double >) |
| calculate the weighted linear regression coefficients for a given for a given data range firstX / firstY / firstW ... lastX / lastY / lastW where the model is | |
| template<class InputItX, class InputItY> | |
| void | jkqtpstatRegression (JKQTPStatRegressionModelType type, InputItX firstX, InputItX lastX, InputItY firstY, InputItY lastY, double &coeffA, double &coeffB, bool fixA=false, bool fixB=false) |
| calculate the linear regression coefficients for a given data range firstX / firstY ... lastX / lastY where the model is defined by type So this function solves the least-squares optimization problem: | |
| jkqtmath_LIB_EXPORT QString | jkqtpstatRegressionModel2Latex (JKQTPStatRegressionModelType type, double a, double b) |
| Generates a LaTeX string for the models from JKQTPStatRegressionModelType in type. | |
| template<class InputItX, class InputItY> | |
| void | jkqtpstatRobustIRLSLinearRegression (InputItX firstX, InputItX lastX, InputItY firstY, InputItY lastY, double &coeffA, double &coeffB, bool fixA=false, bool fixB=false, double p=1.1, int iterations=100) |
| calculate the (robust) iteratively reweighted least-squares (IRLS) estimate for the parameters of the model | |
| template<class InputItX, class InputItY> | |
| void | jkqtpstatRobustIRLSRegression (JKQTPStatRegressionModelType type, InputItX firstX, InputItX lastX, InputItY firstY, InputItY lastY, double &coeffA, double &coeffB, bool fixA=false, bool fixB=false, double p=1.1, int iterations=100) |
| calculate the robust linear regression coefficients for a given data range firstX / firstY ... lastX / lastY where the model is defined by type So this function solves the Lp-norm optimization problem: | |
| template<class InputItX, class InputItY> | |
| double | jkqtpstatSumOfDeviations (InputItX firstX, InputItX lastX, InputItY firstY, InputItY lastY, std::function< double(double)> f) |
| calculates the sum of deviations | |
| template<class InputItX, class InputItY, class InputItW> | |
| double | jkqtpstatWeightedCoefficientOfDetermination (InputItX firstX, InputItX lastX, InputItY firstY, InputItY lastY, InputItW firstW, InputItW lastW, std::function< double(double)> f, std::function< double(double)> fWeightDataToWi=&jkqtp_identity< double >) |
| calculates the weightedcoefficient of determination | |
| template<class InputItX, class InputItY, class InputItW> | |
| void | jkqtpstatWeightedRegression (JKQTPStatRegressionModelType type, InputItX firstX, InputItX lastX, InputItY firstY, InputItY lastY, InputItW firstW, InputItW lastW, double &coeffA, double &coeffB, bool fixA=false, bool fixB=false, std::function< double(double)> fWeightDataToWi=&jkqtp_identity< double >) |
| calculate the robust linear regression coefficients for a given data range firstX / firstY ... lastX / lastY where the model is defined by type So this function solves the Lp-norm optimization problem: | |
| template<class InputItX, class InputItY, class InputItW> | |
| double | jkqtpstatWeightedSumOfDeviations (InputItX firstX, InputItX lastX, InputItY firstY, InputItY lastY, InputItW firstW, InputItW lastW, std::function< double(double)> f, std::function< double(double)> fWeightDataToWi=&jkqtp_identity< double >) |
| calculates the weighted sum of deviations | |
|
strong |
|
inline |
calculates the coefficient of determination 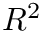
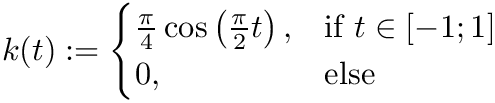
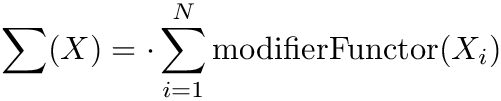
| InputItX | standard iterator type of firstX and lastX. |
| InputItY | standard iterator type of firstY and lastY. |
| firstX | iterator pointing to the first item in the x-dataset to use |
| lastX | iterator pointing behind the last item in the x-dataset to use |
| firstY | iterator pointing to the first item in the y-dataset to use |
| lastY | iterator pointing behind the last item in the y-dataset to use |
| f | function |
![\[ R^2=1-\frac{\sum_i\bigl[y_i-f(x_i)\bigr]^2}{\sum_i\bigl[y_i-\overline{y}\bigr]^2} \]](form_169.png)
![\[ \overline{y}=\frac{1}{N}\cdot\sum_iy_i \]](form_170.png)
| jkqtmath_LIB_EXPORT std::pair< std::function< double(double)>, std::function< double(double)> > jkqtpStatGenerateParameterATransformation | ( | JKQTPStatRegressionModelType | type | ) |
Generates the transformation function for a-parameter (offset, result.first : transform, result.second : back-transform) for each regression model in JKQTPStatRegressionModelType in type.
| jkqtmath_LIB_EXPORT std::pair< std::function< double(double)>, std::function< double(double)> > jkqtpStatGenerateParameterBTransformation | ( | JKQTPStatRegressionModelType | type | ) |
Generates the transformation function for b-parameter (slope, result.first : transform, result.second : back-transform) for each regression model in JKQTPStatRegressionModelType in type.
| jkqtmath_LIB_EXPORT std::function< double(double, double, double)> jkqtpStatGenerateRegressionModel | ( | JKQTPStatRegressionModelType | type | ) |
Generates functors f(x,a,b) for the models from JKQTPStatRegressionModelType in type.
| jkqtmath_LIB_EXPORT std::function< double(double)> jkqtpStatGenerateRegressionModel | ( | JKQTPStatRegressionModelType | type, |
| double | a, | ||
| double | b ) |
Generates functors f(x) for the models from JKQTPStatRegressionModelType in type and binds the parameter values and b to the returned function.
| jkqtmath_LIB_EXPORT std::pair< std::function< double(double)>, std::function< double(double)> > jkqtpStatGenerateTransformation | ( | JKQTPStatRegressionModelType | type | ) |
Generates the transformation function for x-data (result.first ) and y-data (result.second ) for each regression model in JKQTPStatRegressionModelType in type.
|
inline |
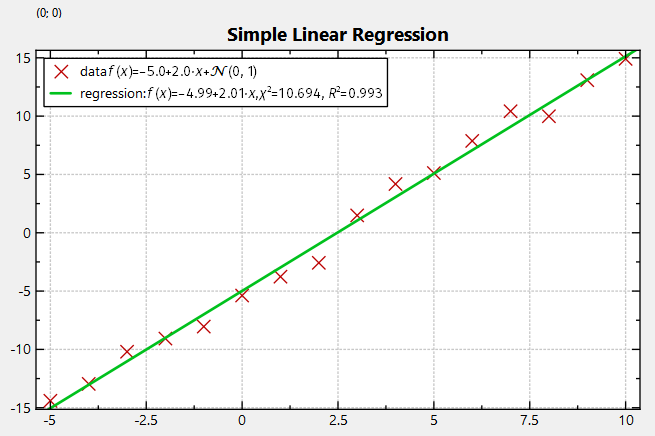
calculate the linear regression coefficients for a given data range firstX / firstY ... lastX / lastY where the model is 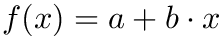
![\[ (a^\ast, b^\ast)=\mathop{\mathrm{arg\;min}}\limits_{a,b}\sum\limits_i\left(y_i-(a+b\cdot x_i)\right)^2 \]](form_132.png)
| InputItX | standard iterator type of firstX and lastX. |
| InputItY | standard iterator type of firstY and lastY. |
| firstX | iterator pointing to the first item in the x-dataset to use | |
| lastX | iterator pointing behind the last item in the x-dataset to use | |
| firstY | iterator pointing to the first item in the y-dataset to use | |
| lastY | iterator pointing behind the last item in the y-dataset to use | |
| [in,out] | coeffA | returns the offset of the linear model |
| [in,out] | coeffB | returns the slope of the linear model |
| fixA | if true, the offset coefficient | |
| fixB | if true, the slope coefficient |
This function computes internally:
![\[ a=\overline{y}-b\cdot\overline{x} \]](form_135.png)
![\[ b=\frac{\sum x_iy_i-N\cdot\overline{x}\cdot\overline{y}}{\sum x_i^2-N\cdot(\overline{x})^2} \]](form_136.png)
|
inline |
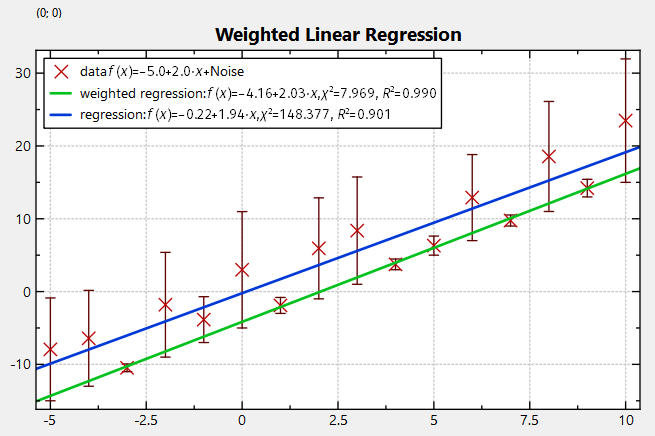
calculate the weighted linear regression coefficients for a given for a given data range firstX / firstY / firstW ... lastX / lastY / lastW where the model is 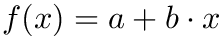
![\[ (a^\ast, b^\ast)=\mathop{\mathrm{arg\;min}}\limits_{a,b}\sum\limits_iw_i^2\cdot\left(y_i-(a+b\cdot x_i)\right)^2 \]](form_137.png)
| InputItX | standard iterator type of firstX and lastX. |
| InputItY | standard iterator type of firstY and lastY. |
| InputItW | standard iterator type of firstW and lastW. |
| firstX | iterator pointing to the first item in the x-dataset to use | |
| lastX | iterator pointing behind the last item in the x-dataset to use | |
| firstY | iterator pointing to the first item in the y-dataset to use | |
| lastY | iterator pointing behind the last item in the y-dataset to use | |
| firstW | iterator pointing to the first item in the weight-dataset to use | |
| lastW | iterator pointing behind the last item in the weight-dataset to use | |
| [in,out] | coeffA | returns the offset of the linear model |
| [in,out] | coeffB | returns the slope of the linear model |
| fixA | if true, the offset coefficient | |
| fixB | if true, the slope coefficient | |
| fWeightDataToWi | an optional function, which is applied to the data from firstW ... lastW to convert them to weight, i.e. wi=fWeightDataToWi(*itW) e.g. if you use data used to draw error bars, you can use jkqtp_inversePropSaveDefault(). The default is jkqtp_identity(), which just returns the values. In the case of jkqtp_inversePropSaveDefault(), a datapoint x,y, has a large weight, if it's error is small and in the case if jkqtp_identity() it's weight is directly proportional to the given value. |
This function internally computes:
![\[ a=\frac{\overline{y}-b\cdot\overline{x}}{\overline{w^2}} \]](form_140.png)
![\[ b=\frac{\overline{w^2}\cdot\overline{x\cdot y}-\overline{x}\cdot\overline{y}}{\overline{x^2}\cdot\overline{w^2}-\overline{x}^2} \]](form_141.png)
Here the averages are defined in terms of a weight vector 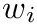
![\[ \overline{x}=\sum\limits_iw_i^2\cdot x_i \]](form_143.png)
![\[ \overline{y}=\sum\limits_iw_i^2\cdot y_i \]](form_144.png)
![\[ \overline{x\cdot y}=\sum\limits_iw_i^2\cdot x_i\cdot y_i \]](form_145.png)
![\[ \overline{x^2}=\sum\limits_iw_i^2\cdot x_i^2 \]](form_146.png)
![\[ \overline{w^2}=\sum\limits_iw_i^2 \]](form_147.png)
|
inline |
calculate the linear regression coefficients for a given data range firstX / firstY ... lastX / lastY where the model is defined by type So this function solves the least-squares optimization problem:
![\[ (a^\ast, b^\ast)=\mathop{\mathrm{arg\;min}}\limits_{a,b}\sum\limits_i\left(y_i-f_{\text{type}}(x_i,a,b)\right)^2 \]](form_165.png)
by reducing it to a linear fit by transforming x- and/or y-data
| InputItX | standard iterator type of firstX and lastX. |
| InputItY | standard iterator type of firstY and lastY. |
| type | model to be fitted | |
| firstX | iterator pointing to the first item in the x-dataset to use | |
| lastX | iterator pointing behind the last item in the x-dataset to use | |
| firstY | iterator pointing to the first item in the y-dataset to use | |
| lastY | iterator pointing behind the last item in the y-dataset to use | |
| [in,out] | coeffA | returns the offset of the linear model |
| [in,out] | coeffB | returns the slope of the linear model |
| fixA | if true, the offset coefficient | |
| fixB | if true, the slope coefficient |
This function computes internally first transforms the data, as appropriate to fit the model defined by type and then calls jkqtpstatLinearRegression() to obtain the parameters. The output parameters are transformed, so they can be used with jkqtpStatGenerateRegressionModel() to generate a functor that evaluates the model
| jkqtmath_LIB_EXPORT QString jkqtpstatRegressionModel2Latex | ( | JKQTPStatRegressionModelType | type, |
| double | a, | ||
| double | b ) |
Generates a LaTeX string for the models from JKQTPStatRegressionModelType in type.
|
inline |
calculate the (robust) iteratively reweighted least-squares (IRLS) estimate for the parameters of the model 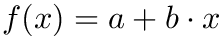
![\[ (a^\ast,b^\ast)=\mathop{\mathrm{arg\;min}}\limits_{a,b}\sum\limits_i|a+b\cdot x_i-y_i|^p \]](form_148.png)
| InputItX | standard iterator type of firstX and lastX. |
| InputItY | standard iterator type of firstY and lastY. |
| firstX | iterator pointing to the first item in the x-dataset to use | |
| lastX | iterator pointing behind the last item in the x-dataset to use | |
| firstY | iterator pointing to the first item in the y-dataset to use | |
| lastY | iterator pointing behind the last item in the y-dataset to use | |
| [in,out] | coeffA | returns the offset of the linear model |
| [in,out] | coeffB | returns the slope of the linear model |
| fixA | if true, the offset coefficient | |
| fixB | if true, the slope coefficient | |
| p | regularization parameter, the optimization problem is formulated in the | |
| iterations | the number of iterations the IRLS algorithm performs |
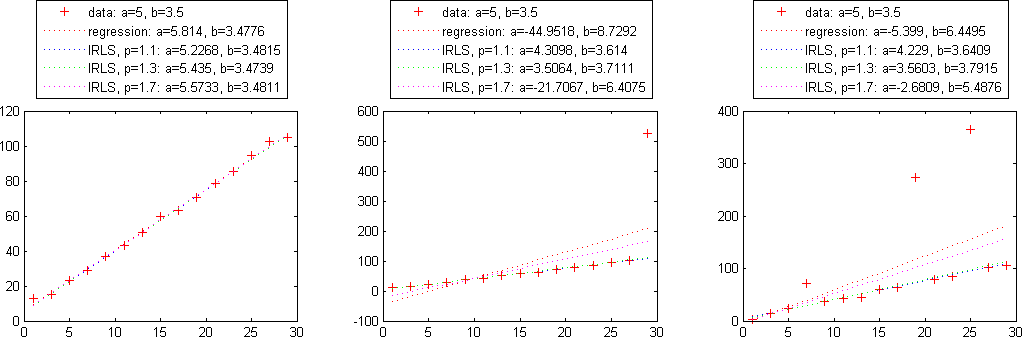
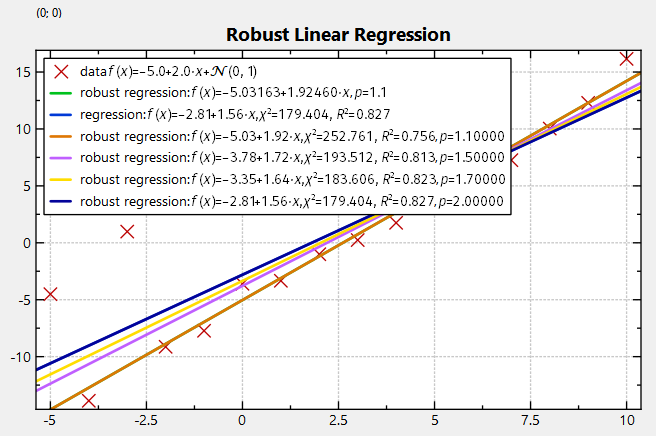
This is a simple form of the IRLS algorithm to estimate the parameters a and b in a linear model 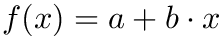
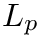
![\[ (a^\ast,b^\ast)=\mathop{\mathrm{arg\;min}}\limits_{a,b}\sum\limits_i|a+b\cdot x_i-y_i|^p \]](form_148.png)
by iteratively optimization weights 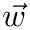
![\[ (a_n,b_n)=\mathop{\mathrm{arg\;min}}\limits_{a,b}\sum\limits_i|a+b\cdot x_i-y_i|^{(p-2)}\cdot|a+b\cdot x_i-y_i|^2 \]](form_152.png)
The IRLS-algorithm works as follows:
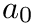
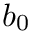
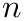
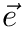
![\[ e_i = a+b\cdot x_i -y_i \]](form_157.png)
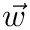
![\[ w_i=|e_i|^{(p-2)/2} \]](form_159.png)
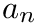
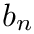
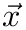
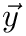
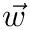
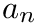
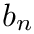
|
inline |
calculate the robust linear regression coefficients for a given data range firstX / firstY ... lastX / lastY where the model is defined by type So this function solves the Lp-norm optimization problem:
![\[ (a^\ast, b^\ast)=\mathop{\mathrm{arg\;min}}\limits_{a,b}\sum\limits_i|y_i-f_{\text{type}}(x_i,a,b)|^p \]](form_166.png)
by reducing it to a linear fit by transforming x- and/or y-data
| InputItX | standard iterator type of firstX and lastX. |
| InputItY | standard iterator type of firstY and lastY. |
| type | model to be fitted | |
| firstX | iterator pointing to the first item in the x-dataset to use | |
| lastX | iterator pointing behind the last item in the x-dataset to use | |
| firstY | iterator pointing to the first item in the y-dataset to use | |
| lastY | iterator pointing behind the last item in the y-dataset to use | |
| [in,out] | coeffA | returns the offset of the linear model |
| [in,out] | coeffB | returns the slope of the linear model |
| fixA | if true, the offset coefficient | |
| fixB | if true, the slope coefficient | |
| p | regularization parameter, the optimization problem is formulated in the | |
| iterations | the number of iterations the IRLS algorithm performs |
This function computes internally first transforms the data, as appropriate to fit the model defined by type and then calls jkqtpstatRobustIRLSLinearRegression() to obtain the parameters. The output parameters are transformed, so they can be used with jkqtpStatGenerateRegressionModel() to generate a functor that evaluates the model
|
inline |
calculates the sum of deviations 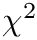
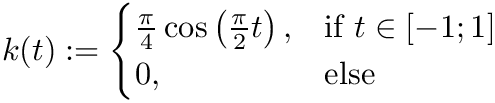
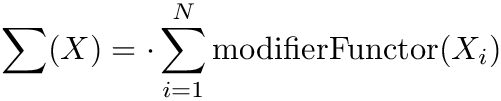
| InputItX | standard iterator type of firstX and lastX. |
| InputItY | standard iterator type of firstY and lastY. |
| firstX | iterator pointing to the first item in the x-dataset to use |
| lastX | iterator pointing behind the last item in the x-dataset to use |
| firstY | iterator pointing to the first item in the y-dataset to use |
| lastY | iterator pointing behind the last item in the y-dataset to use |
| f | function |
![\[ \chi^2=\sum_i\bigl[y_i-f(x_i)\bigr]^2 \]](form_176.png)
|
inline |
calculates the weightedcoefficient of determination 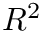
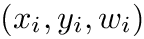
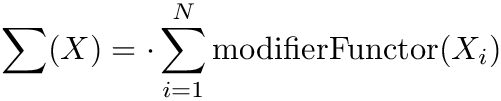
| InputItX | standard iterator type of firstX and lastX. |
| InputItY | standard iterator type of firstY and lastY. |
| InputItW | standard iterator type of firstW and lastW. |
| firstX | iterator pointing to the first item in the x-dataset to use |
| lastX | iterator pointing behind the last item in the x-dataset to use |
| firstY | iterator pointing to the first item in the y-dataset to use |
| lastY | iterator pointing behind the last item in the y-dataset to use |
| firstW | iterator pointing to the first item in the weight-dataset to use |
| lastW | iterator pointing behind the last item in the weight-dataset to use |
| f | function |
| fWeightDataToWi | an optional function, which is applied to the data from firstW ... lastW to convert them to weight, i.e. wi=fWeightDataToWi(*itW) e.g. if you use data used to draw error bars, you can use jkqtp_inversePropSaveDefault(). The default is jkqtp_identity(), which just returns the values. In the case of jkqtp_inversePropSaveDefault(), a datapoint x,y, has a large weight, if it's error is small and in the case if jkqtp_identity() it's weight is directly proportional to the given value. |
![\[ R^2=1-\frac{\sum_iw_i^2\bigl[y_i-f(x_i)\bigr]^2}{\sum_iw_i^2\bigl[y_i-\overline{y}\bigr]^2} \]](form_172.png)
![\[ \overline{y}=\frac{1}{N}\cdot\sum_iw_iy_i \]](form_173.png)
![\[ \sum_iw_i=1 \]](form_174.png)
|
inline |
calculate the robust linear regression coefficients for a given data range firstX / firstY ... lastX / lastY where the model is defined by type So this function solves the Lp-norm optimization problem:
![\[ (a^\ast, b^\ast)=\mathop{\mathrm{arg\;min}}\limits_{a,b}\sum\limits_iw_i^2\left(y_i-f_{\text{type}}(x_i,a,b)\right)^2 \]](form_167.png)
by reducing it to a linear fit by transforming x- and/or y-data
| InputItX | standard iterator type of firstX and lastX. |
| InputItY | standard iterator type of firstY and lastY. |
| InputItW | standard iterator type of firstW and lastW. |
| type | model to be fitted | |
| firstX | iterator pointing to the first item in the x-dataset to use | |
| lastX | iterator pointing behind the last item in the x-dataset to use | |
| firstY | iterator pointing to the first item in the y-dataset to use | |
| lastY | iterator pointing behind the last item in the y-dataset to use | |
| firstW | iterator pointing to the first item in the weight-dataset to use | |
| lastW | iterator pointing behind the last item in the weight-dataset to use | |
| [in,out] | coeffA | returns the offset of the linear model |
| [in,out] | coeffB | returns the slope of the linear model |
| fixA | if true, the offset coefficient | |
| fixB | if true, the slope coefficient | |
| fWeightDataToWi | an optional function, which is applied to the data from firstW ... lastW to convert them to weight, i.e. wi=fWeightDataToWi(*itW) e.g. if you use data used to draw error bars, you can use jkqtp_inversePropSaveDefault(). The default is jkqtp_identity(), which just returns the values. In the case of jkqtp_inversePropSaveDefault(), a datapoint x,y, has a large weight, if it's error is small and in the case if jkqtp_identity() it's weight is directly proportional to the given value. |
This function computes internally first transforms the data, as appropriate to fit the model defined by type and then calls jkqtpstatLinearWeightedRegression() to obtain the parameters. The output parameters are transformed, so they can be used with jkqtpStatGenerateRegressionModel() to generate a functor that evaluates the model
|
inline |
calculates the weighted sum of deviations 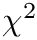
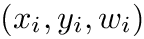
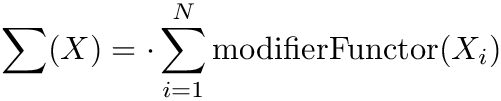
| InputItX | standard iterator type of firstX and lastX. |
| InputItY | standard iterator type of firstY and lastY. |
| InputItW | standard iterator type of firstW and lastW. |
| firstX | iterator pointing to the first item in the x-dataset to use |
| lastX | iterator pointing behind the last item in the x-dataset to use |
| firstY | iterator pointing to the first item in the y-dataset to use |
| lastY | iterator pointing behind the last item in the y-dataset to use |
| firstW | iterator pointing to the first item in the weight-dataset to use |
| lastW | iterator pointing behind the last item in the weight-dataset to use |
| f | function |
| fWeightDataToWi | an optional function, which is applied to the data from firstW ... lastW to convert them to weight, i.e. wi=fWeightDataToWi(*itW) e.g. if you use data used to draw error bars, you can use jkqtp_inversePropSaveDefault(). The default is jkqtp_identity(), which just returns the values. In the case of jkqtp_inversePropSaveDefault(), a datapoint x,y, has a large weight, if it's error is small and in the case if jkqtp_identity() it's weight is directly proportional to the given value. |
![\[ \chi^2=\sum_iw_i^2\cdot\bigl[y_i-f(x_i)\bigr]^2 \]](form_177.png)