Collaboration diagram for Mathematical Functions & Tools:

Classes
struct	JKQTPPolynomialFunctor
	a C++-functor, which evaluates a polynomial More...

Macros
#define	JKQTP_DOUBLE_EPSILON (std::numeric_limits<double>::epsilon())
	double-value epsilon

#define	JKQTP_DOUBLE_NAN (std::numeric_limits<double>::signaling_NaN())
	double-value NotANumber

#define	JKQTP_EPSILON JKQTP_DOUBLE_EPSILON
	double-value NotANumber

#define	JKQTP_FLOAT_EPSILON (std::numeric_limits<float>::epsilon())
	float-value epsilon

#define	JKQTP_FLOAT_NAN (std::numeric_limits<float>::signaling_NaN())
	float-value NotANumber

#define	JKQTP_NAN JKQTP_DOUBLE_NAN
	double-value NotANumber

#define	JKQTPSTATISTICS_LN10 2.30258509299404568402
	$\mbox{ln}(10)=2.30258509299404568402...$

#define	JKQTPSTATISTICS_PI 3.14159265358979323846
	$\pi=3.14159...$

#define	JKQTPSTATISTICS_SQRT_2PI 2.50662827463
	$\sqrt{2\pi}=2.50662827463$

Functions
bool	jkqtp_approximatelyEqual (double a, double b, double epsilon=2.0 *JKQTP_DOUBLE_EPSILON)
	compare two doubles a and b for euqality, where any difference smaller than epsilon is seen as equality

bool	jkqtp_approximatelyEqual (float a, float b, float epsilon=2.0f *JKQTP_FLOAT_EPSILON)
	compare two floats a and b for euqality, where any difference smaller than epsilon is seen as equality

bool	jkqtp_approximatelyUnequal (double a, double b, double epsilon=2.0 *JKQTP_DOUBLE_EPSILON)
	compare two doubles a and b for uneuqality, where any difference smaller than epsilon is seen as equality

bool	jkqtp_approximatelyUnequal (float a, float b, float epsilon=2.0f *JKQTP_FLOAT_EPSILON)
	compare two floats a and b for uneuqality, where any difference smaller than epsilon is seen as equality

template<typename T >
T	jkqtp_bounded (T min, T v, T max)
	limits a value v to the given range min ... max

template<typename T , typename TIn >
T	jkqtp_bounded (TIn v)
	limits a value v to the range of the given type T , i.e. `std::numeric_limits<T>::min()` ... `std::numeric_limits<T>::max()`

template<typename T >
T	jkqtp_boundedRoundTo (const double &v)
	round a double v using round() and convert it to a specified type T (static_cast!). Finally the value is bounded to the range `std::numeric_limits<T>::min()` ... `std::numeric_limits<T>::max()`

template<typename T >
T	jkqtp_boundedRoundTo (T min, const double &v, T max)
	round a double v using round() and convert it to a specified type T (static_cast!). Finally the value is bounded to the range min ... max

template<typename T >
T	jkqtp_ceilTo (const double &v)
	round a double v using ceil() and convert it to a specified type T (static_cast!)

template<class T = int>
T	jkqtp_combination (T n, T k)
	Calculates a combination $\left(\stackrel{n}{k}\right)=\frac{n!}{k!\cdot(n-k)!}$ .

void	jkqtp_combine_hash (std::size_t &seed, std::size_t hsh)
	can be used to build a hash-values from several hash-values

template<class T >
T	jkqtp_cube (T x)
	cube of a number

double	jkqtp_distance (const QPoint &p1, const QPoint &p2)
	calculate the distance between two QPoint points

double	jkqtp_distance (const QPointF &p1, const QPointF &p2)
	calculate the distance between two QPointF points

JKQTCOMMON_LIB_EXPORT void	jkqtp_estimateFraction (double input, int &sign, uint64_t &intpart, uint64_t &num, uint64_t &denom, unsigned int precision=9)
	calculates numeratur integer part intpart , num and denominator denom of a fraction, representing a given floating-point number input

template<class T = int>
T	jkqtp_factorial (T n)
	Calculates a factorial $n!=n\cdot(n-1)\cdot(n-2)\cdot...\cdot2\cdot1$ .

template<typename T >
T	jkqtp_floorTo (const double &v)
	round a double v using floor() and convert it to a specified type T (static_cast!)

double	jkqtp_gaussdist (double x, double mu=0.0, double sigma=1.0)
	evaluates a gaussian propability density function

JKQTCOMMON_LIB_EXPORT uint64_t	jkqtp_gcd (uint64_t a, uint64_t b)
	calculate the grwates common divisor (GCD) of a and b

template<class PolyItP >
std::function< double(double)>	jkqtp_generatePolynomialModel (PolyItP firstP, PolyItP lastP)
	returns a C++-functor, which evaluates a polynomial

template<class T >
void	jkqtp_hash_combine (std::size_t &seed, const T &v)
	can be used to build a hash-values from several hash-values

template<typename T >
T	jkqtp_identity (const T &v)
	returns the given value v (i.e. identity function)

template<typename T >
T	jkqtp_inverseProp (const T &v)
	returns the inversely proportional value 1/v of v

template<typename T >
T	jkqtp_inversePropSave (const T &v, const T &absMinV)
	returns the inversely proportional value 1/v of v and ensures that $\|v\|\geq \mbox{absMinV}$

template<typename T >
T	jkqtp_inversePropSaveDefault (const T &v)
	returns the inversely proportional value 1/v of v and ensures that $\|v\|\geq \mbox{absMinV}$ , uses `absMinV=std::numeric_limits<T>::epsilon()*100`.0

double	jkqtp_j0 (double x)
	j0() function (without compiler issues)

double	jkqtp_j1 (double x)
	j1() function (without compiler issues)

double	jkqtp_jn (int n, double x)
	jn() function (without compiler issues)

template<class T >
std::function< T(T)>	jkqtp_makeBernstein (int n, int i)
	creates a functor that evaluates the Bernstein polynomial $B_i^n(t):=\left(\stackrel{n}{i}\right)\cdot t^i\cdot(1-t)^{n-1},\ \ \ \ 0\leq i\leq n$

template<class PolyItP >
double	jkqtp_polyEval (double x, PolyItP firstP, PolyItP lastP)
	evaluate a polynomial $f(x)=\sum\limits_{i=0}^Pp_ix^i$ with taken from the range firstP ... lastP

template<class PolyItP >
QString	jkqtp_polynomialModel2Latex (PolyItP firstP, PolyItP lastP)
	Generates a LaTeX string for the polynomial model with the coefficients firstP ... lastP.

template<class T >
T	jkqtp_pow4 (T x)
	4-th power of a number

template<class T >
T	jkqtp_pow5 (T x)
	5-th power of a number

template<class T >
T	jkqtp_reversed (const T &l)
	returns the reversed containter l

template<typename T >
T	jkqtp_roundTo (const double &v)
	round a double v using round() and convert it to a specified type T (static_cast!)

double	jkqtp_roundToDigits (const double &v, const int decDigits)
	round a double v using round() to a given number of decimal digits

template<class T >
T	jkqtp_sign (T x)
	calculates the sign of number x (-1 for x<0 and +1 for x>=0)

template<typename T >
T	jkqtp_sqr (const T &v)
	returns the quare of the value v, i.e. `v*v`

template<>
constexpr double	jkqtp_todouble (const bool &d)
	converts a boolean to a double, is used to convert boolean to double by JKQTPDatastore

template<typename T >
constexpr double	jkqtp_todouble (const T &d)
	converts a boolean to a double, is used to convert boolean to double by JKQTPDatastore

template<typename T >
T	jkqtp_truncTo (const double &v)
	round a double v using trunc() and convert it to a specified type T (static_cast!)

double	jkqtp_y0 (double x)
	y0() function (without compiler issues)

double	jkqtp_y1 (double x)
	y1() function (without compiler issues)

double	jkqtp_yn (int n, double x)
	yn() function (without compiler issues)

template<typename T >
bool	JKQTPIsOKFloat (T v)
	check whether the dlotaing point number is OK (i.e. non-inf, non-NAN)

Detailed Description

This group assembles a variety of mathematical tool functions that are used in different places.

Macro Definition Documentation

◆ JKQTP_DOUBLE_EPSILON

#define JKQTP_DOUBLE_EPSILON (std::numeric_limits<double>::epsilon())

double-value epsilon

◆ JKQTP_DOUBLE_NAN

#define JKQTP_DOUBLE_NAN (std::numeric_limits<double>::signaling_NaN())

double-value NotANumber

◆ JKQTP_EPSILON

#define JKQTP_EPSILON JKQTP_DOUBLE_EPSILON

double-value NotANumber

◆ JKQTP_FLOAT_EPSILON

#define JKQTP_FLOAT_EPSILON (std::numeric_limits<float>::epsilon())

float-value epsilon

◆ JKQTP_FLOAT_NAN

#define JKQTP_FLOAT_NAN (std::numeric_limits<float>::signaling_NaN())

float-value NotANumber

◆ JKQTP_NAN

#define JKQTP_NAN JKQTP_DOUBLE_NAN

double-value NotANumber

◆ JKQTPSTATISTICS_LN10

#define JKQTPSTATISTICS_LN10 2.30258509299404568402

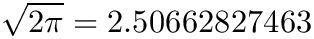
$\mbox{ln}(10)=2.30258509299404568402...$

◆ JKQTPSTATISTICS_PI

#define JKQTPSTATISTICS_PI 3.14159265358979323846

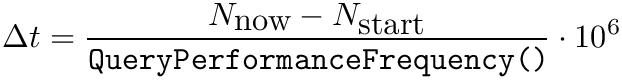
$\pi=3.14159...$

◆ JKQTPSTATISTICS_SQRT_2PI

#define JKQTPSTATISTICS_SQRT_2PI 2.50662827463

$\sqrt{2\pi}=2.50662827463$

Function Documentation

◆ jkqtp_approximatelyEqual() [1/2]

bool jkqtp_approximatelyEqual	(	double	a,
		double	b,
		double	epsilon = `2.0*JKQTP_DOUBLE_EPSILON`
	)

inline

compare two doubles a and b for euqality, where any difference smaller than epsilon is seen as equality

◆ jkqtp_approximatelyEqual() [2/2]

bool jkqtp_approximatelyEqual	(	float	a,
		float	b,
		float	epsilon = `2.0f*JKQTP_FLOAT_EPSILON`
	)

inline

compare two floats a and b for euqality, where any difference smaller than epsilon is seen as equality

◆ jkqtp_approximatelyUnequal() [1/2]

bool jkqtp_approximatelyUnequal	(	double	a,
		double	b,
		double	epsilon = `2.0*JKQTP_DOUBLE_EPSILON`
	)

inline

compare two doubles a and b for uneuqality, where any difference smaller than epsilon is seen as equality

◆ jkqtp_approximatelyUnequal() [2/2]

bool jkqtp_approximatelyUnequal	(	float	a,
		float	b,
		float	epsilon = `2.0f*JKQTP_FLOAT_EPSILON`
	)

inline

compare two floats a and b for uneuqality, where any difference smaller than epsilon is seen as equality

◆ jkqtp_bounded() [1/2]

template<typename T >

T jkqtp_bounded	(	T	min,
		T	v,
		T	max
	)

inline

limits a value v to the given range min ... max

Template Parameters

T	a numeric datatype (int, double, ...)

Parameters

min	minimum output value
v	the value to round and cast
max	maximum output value

◆ jkqtp_bounded() [2/2]

template<typename T , typename TIn >

T jkqtp_bounded ( TIn v )

inline

limits a value v to the range of the given type T , i.e. std::numeric_limits<T>::min() ... std::numeric_limits<T>::max()

Template Parameters

T	a numeric datatype (int, double, ...) for the output
TIn	a numeric datatype (int, double, ...) or the input v

Parameters

v	the value to round and cast

Note: As a special feature, this function detectes whether one of T or TIn are unsigned and then cmpares against a limit of 0 instead of std::numeric_limits<T>::min() .

◆ jkqtp_boundedRoundTo() [1/2]

template<typename T >

T jkqtp_boundedRoundTo ( const double & v )

inline

round a double v using round() and convert it to a specified type T (static_cast!). Finally the value is bounded to the range std::numeric_limits<T>::min() ... std::numeric_limits<T>::max()

Template Parameters

T	a numeric datatype (int, double, ...)

Parameters

v	the value to round and cast

this is equivalent to

jkqtp_boundedRoundTo<T>(std::numeric_limits<T>::min(), v, std::numeric_limits<T>::max())

◆ jkqtp_boundedRoundTo() [2/2]

template<typename T >

T jkqtp_boundedRoundTo	(	T	min,
		const double &	v,
		T	max
	)

inline

round a double v using round() and convert it to a specified type T (static_cast!). Finally the value is bounded to the range min ... max

Template Parameters

T	a numeric datatype (int, double, ...)

Parameters

min	minimum output value
v	the value to round and cast
max	maximum output value

this is equivalent to

qBound(min, static_cast<T>(round(v)), max);

◆ jkqtp_ceilTo()

template<typename T >

T jkqtp_ceilTo ( const double & v )

inline

round a double v using ceil() and convert it to a specified type T (static_cast!)

Template Parameters

T	a numeric datatype (int, double, ...)

Parameters

v	the value to ceil and cast

this is equivalent to

static_cast<T>(ceil(v));

◆ jkqtp_combination()

template<class T = int>

T jkqtp_combination	(	T	n,
		T	k
	)

inline

Calculates a combination 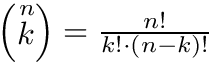$\left(\stackrel{n}{k}\right)=\frac{n!}{k!\cdot(n-k)!}$ .

◆ jkqtp_combine_hash()

void jkqtp_combine_hash	(	std::size_t &	seed,
		std::size_t	hsh
	)

inline

can be used to build a hash-values from several hash-values

std::size_t seed=0;
jkqtp_combine_hash(seed, qHash(valA));
jkqtp_combine_hash(seed, qHash(valB));
//...
// finally seed contains the combined hash

◆ jkqtp_cube()

template<class T >

T jkqtp_cube ( T x )

inline

cube of a number

◆ jkqtp_distance() [1/2]

double jkqtp_distance	(	const QPoint &	p1,
		const QPoint &	p2
	)

inline

calculate the distance between two QPoint points

◆ jkqtp_distance() [2/2]

double jkqtp_distance	(	const QPointF &	p1,
		const QPointF &	p2
	)

inline

calculate the distance between two QPointF points

◆ jkqtp_estimateFraction()

JKQTCOMMON_LIB_EXPORT void jkqtp_estimateFraction	(	double	input,
		int &	sign,
		uint64_t &	intpart,
		uint64_t &	num,
		uint64_t &	denom,
		unsigned int	precision = `9`
	)

calculates numeratur integer part intpart , num and denominator denom of a fraction, representing a given floating-point number input

◆ jkqtp_factorial()

template<class T = int>

T jkqtp_factorial ( T n )

inline

Calculates a factorial 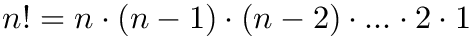$n!=n\cdot(n-1)\cdot(n-2)\cdot...\cdot2\cdot1$ .

◆ jkqtp_floorTo()

template<typename T >

T jkqtp_floorTo ( const double & v )

inline

round a double v using floor() and convert it to a specified type T (static_cast!)

Template Parameters

T	a numeric datatype (int, double, ...)

Parameters

v	the value to floor and cast

this is equivalent to

static_cast<T>(floor(v));

◆ jkqtp_gaussdist()

double jkqtp_gaussdist	(	double	x,
		double	mu = `0.0`,
		double	sigma = `1.0`
	)

inline

evaluates a gaussian propability density function

$f(x,\mu, \sigma)=\frac{1}{\sqrt{2\pi\sigma^2}}\cdot\exp\left(-\frac{(x-\mu)^2}{2\sigma^2}\right)$

◆ jkqtp_gcd()

JKQTCOMMON_LIB_EXPORT uint64_t jkqtp_gcd	(	uint64_t	a,
		uint64_t	b
	)

calculate the grwates common divisor (GCD) of a and b

◆ jkqtp_generatePolynomialModel()

template<class PolyItP >

std::function< double(double)> jkqtp_generatePolynomialModel	(	PolyItP	firstP,
		PolyItP	lastP
	)

inline

returns a C++-functor, which evaluates a polynomial

Template Parameters

PolyItP iterator for the polynomial coefficients

Parameters

firstP	points to the first polynomial coefficient (i.e. the offset with )
lastP	points behind the last polynomial coefficient

◆ jkqtp_hash_combine()

template<class T >

void jkqtp_hash_combine	(	std::size_t &	seed,
		const T &	v
	)

inline

can be used to build a hash-values from several hash-values

std::size_t seed=0;
jkqtp_hash_combine(seed, valA);
jkqtp_hash_combine(seed, valB);
//...
// finally seed contains the combined hash

◆ jkqtp_identity()

template<typename T >

T jkqtp_identity ( const T & v )

inline

returns the given value v (i.e. identity function)

◆ jkqtp_inverseProp()

template<typename T >

T jkqtp_inverseProp ( const T & v )

inline

returns the inversely proportional value 1/v of v

◆ jkqtp_inversePropSave()

template<typename T >

T jkqtp_inversePropSave	(	const T &	v,
		const T &	absMinV
	)

inline

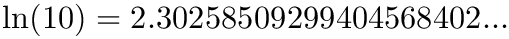
returns the inversely proportional value 1/v of v and ensures that $|v|\geq \mbox{absMinV}$

◆ jkqtp_inversePropSaveDefault()

template<typename T >

T jkqtp_inversePropSaveDefault ( const T & v )

inline

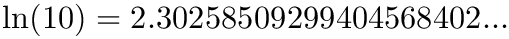
returns the inversely proportional value 1/v of v and ensures that $|v|\geq \mbox{absMinV}$ , uses absMinV=std::numeric_limits<T>::epsilon()*100.0

◆ jkqtp_j0()

double jkqtp_j0 ( double x )

inline

j0() function (without compiler issues)

◆ jkqtp_j1()

double jkqtp_j1 ( double x )

inline

j1() function (without compiler issues)

◆ jkqtp_jn()

double jkqtp_jn	(	int	n,
		double	x
	)

inline

jn() function (without compiler issues)

◆ jkqtp_makeBernstein()

template<class T >

std::function< T(T)> jkqtp_makeBernstein	(	int	n,
		int	i
	)

creates a functor that evaluates the Bernstein polynomial 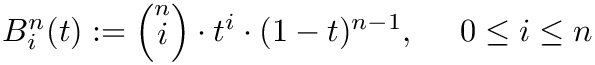$B_i^n(t):=\left(\stackrel{n}{i}\right)\cdot t^i\cdot(1-t)^{n-1},\ \ \ \ 0\leq i\leq n$

◆ jkqtp_polyEval()

template<class PolyItP >

double jkqtp_polyEval	(	double	x,
		PolyItP	firstP,
		PolyItP	lastP
	)

inline

evaluate a polynomial 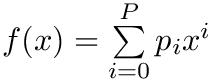$f(x)=\sum\limits_{i=0}^Pp_ix^i$ with taken from the range firstP ... lastP

Template Parameters

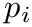
PolyItP iterator for the polynomial coefficients

Parameters

x	where to evaluate
firstP	points to the first polynomial coefficient (i.e. the offset with )
lastP	points behind the last polynomial coefficient

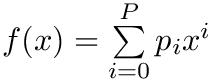
Returns: value of polynomial $f(x)=\sum\limits_{i=0}^Pp_ix^i$ at location x

◆ jkqtp_polynomialModel2Latex()

template<class PolyItP >

QString jkqtp_polynomialModel2Latex	(	PolyItP	firstP,
		PolyItP	lastP
	)

Generates a LaTeX string for the polynomial model with the coefficients firstP ... lastP.

Template Parameters

PolyItP iterator for the polynomial coefficients

Parameters

firstP	points to the first polynomial coefficient (i.e. the offset with )
lastP	points behind the last polynomial coefficient

◆ jkqtp_pow4()

template<class T >

T jkqtp_pow4 ( T x )

inline

4-th power of a number

◆ jkqtp_pow5()

template<class T >

T jkqtp_pow5 ( T x )

inline

5-th power of a number

◆ jkqtp_reversed()

template<class T >

T jkqtp_reversed ( const T & l )

inline

returns the reversed containter l

◆ jkqtp_roundTo()

template<typename T >

T jkqtp_roundTo ( const double & v )

inline

round a double v using round() and convert it to a specified type T (static_cast!)

Template Parameters

T	a numeric datatype (int, double, ...)

Parameters

v	the value to round and cast

this is equivalent to

static_cast<T>(round(v));

◆ jkqtp_roundToDigits()

double jkqtp_roundToDigits	(	const double &	v,
		const int	decDigits
	)

inline

round a double v using round() to a given number of decimal digits

Parameters

v	the value to round and cast
decDigits	number of decimal digits, i.e. precision of the result

this is equivalent to

round(v * pow(10.0,(double)decDigits))/pow(10.0,(double)decDigits);

◆ jkqtp_sign()

template<class T >

T jkqtp_sign ( T x )

inline

calculates the sign of number x (-1 for x<0 and +1 for x>=0)

◆ jkqtp_sqr()

template<typename T >

T jkqtp_sqr ( const T & v )

inline

returns the quare of the value v, i.e. v*v

◆ jkqtp_todouble() [1/2]

template<>

constexpr double jkqtp_todouble ( const bool & d )

inlineconstexpr

converts a boolean to a double, is used to convert boolean to double by JKQTPDatastore

Specialisation of the generic template jkqtp_todouble() with (true -> 1.0, false -> 0.0)

◆ jkqtp_todouble() [2/2]

template<typename T >

constexpr double jkqtp_todouble ( const T & d )

inlineconstexpr

converts a boolean to a double, is used to convert boolean to double by JKQTPDatastore

This function uses static_cast<double>() by default, but certain specializations (e.g. for bool) are readily available.

Here is the caller graph for this function:

◆ jkqtp_truncTo()

template<typename T >

T jkqtp_truncTo ( const double & v )

inline

round a double v using trunc() and convert it to a specified type T (static_cast!)

Template Parameters

T	a numeric datatype (int, double, ...)

Parameters

v	the value to trunc and cast

this is equivalent to

static_cast<T>(trunc(v));

◆ jkqtp_y0()

double jkqtp_y0 ( double x )

inline

y0() function (without compiler issues)

◆ jkqtp_y1()

double jkqtp_y1 ( double x )

inline

y1() function (without compiler issues)

◆ jkqtp_yn()

double jkqtp_yn	(	int	n,
		double	x
	)

inline

yn() function (without compiler issues)

◆ JKQTPIsOKFloat()

template<typename T >

bool JKQTPIsOKFloat ( T v )

inline

check whether the dlotaing point number is OK (i.e. non-inf, non-NAN)

Classes

Macros

Functions

Detailed Description

Macro Definition Documentation

◆ JKQTP_DOUBLE_EPSILON

◆ JKQTP_DOUBLE_NAN

◆ JKQTP_EPSILON

◆ JKQTP_FLOAT_EPSILON

◆ JKQTP_FLOAT_NAN

◆ JKQTP_NAN

◆ JKQTPSTATISTICS_LN10

◆ JKQTPSTATISTICS_PI

◆ JKQTPSTATISTICS_SQRT_2PI

Function Documentation

◆ jkqtp_approximatelyEqual() [1/2]

◆ jkqtp_approximatelyEqual() [2/2]

◆ jkqtp_approximatelyUnequal() [1/2]

◆ jkqtp_approximatelyUnequal() [2/2]

◆ jkqtp_bounded() [1/2]

◆ jkqtp_bounded() [2/2]

◆ jkqtp_boundedRoundTo() [1/2]

◆ jkqtp_boundedRoundTo() [2/2]

◆ jkqtp_ceilTo()

◆ jkqtp_combination()

◆ jkqtp_combine_hash()

◆ jkqtp_cube()

◆ jkqtp_distance() [1/2]

◆ jkqtp_distance() [2/2]

◆ jkqtp_estimateFraction()

◆ jkqtp_factorial()

◆ jkqtp_floorTo()

◆ jkqtp_gaussdist()

◆ jkqtp_gcd()

◆ jkqtp_generatePolynomialModel()

◆ jkqtp_hash_combine()

◆ jkqtp_identity()

◆ jkqtp_inverseProp()

◆ jkqtp_inversePropSave()

◆ jkqtp_inversePropSaveDefault()

◆ jkqtp_j0()

◆ jkqtp_j1()

◆ jkqtp_jn()

◆ jkqtp_makeBernstein()

◆ jkqtp_polyEval()

◆ jkqtp_polynomialModel2Latex()

◆ jkqtp_pow4()

◆ jkqtp_pow5()

◆ jkqtp_reversed()

◆ jkqtp_roundTo()

◆ jkqtp_roundToDigits()

◆ jkqtp_sign()

◆ jkqtp_sqr()

◆ jkqtp_todouble() [1/2]

◆ jkqtp_todouble() [2/2]

◆ jkqtp_truncTo()

◆ jkqtp_y0()

◆ jkqtp_y1()

◆ jkqtp_yn()

◆ JKQTPIsOKFloat()