Collaboration diagram for Polynomial Fits/Regression:

Functions
template<class InputItX , class InputItY , class OutputItP >
void	jkqtpstatPolyFit (InputItX firstX, InputItX lastX, InputItY firstY, InputItY lastY, size_t P, OutputItP firstRes)
	fits (in a least-squares sense) a polynomial $f(x)=\sum\limits_{i=0}^Pp_ix^i$ of order P to a set of N data pairs

Detailed Description

Function Documentation

◆ jkqtpstatPolyFit()

template<class InputItX , class InputItY , class OutputItP >

void jkqtpstatPolyFit	(	InputItX	firstX,
		InputItX	lastX,
		InputItY	firstY,
		InputItY	lastY,
		size_t	P,
		OutputItP	firstRes
	)

inline

fits (in a least-squares sense) a polynomial 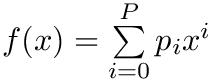$f(x)=\sum\limits_{i=0}^Pp_ix^i$ of order P to a set of N data pairs

Template Parameters

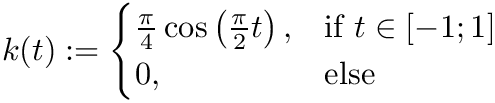
InputItX	standard iterator type of firstX and lastX.
InputItY	standard iterator type of firstY and lastY.
OutputItP	output iterator for the polynomial coefficients

Parameters

	firstX	iterator pointing to the first item in the x-dataset to use
	lastX	iterator pointing behind the last item in the x-dataset to use
	firstY	iterator pointing to the first item in the y-dataset to use
	lastY	iterator pointing behind the last item in the y-dataset to use
	P	degree of the polynomial (P>=N !!!)
[out]	firstRes	Iterator (of type OutputItP ), which receives the (P+1)-entry vector with the polynomial coefficients

This function uses jkqtpstatLinSolve() to solve the system of equations

$\begin{bmatrix} y_1\\ y_2\\ y_3 \\ \vdots \\ y_n \end{bmatrix}= \begin{bmatrix} 1 & x_1 & x_1^2 & \dots & x_1^P \\ 1 & x_2 & x_2^2 & \dots & x_2^P\\ 1 & x_3 & x_3^2 & \dots & x_3^P \\ \vdots & \vdots & \vdots & & \vdots \\ 1 & x_n & x_n^2 & \dots & x_n^P \end{bmatrix} \begin{bmatrix} p_0\\ p_1\\ p_2\\ \vdots \\ p_P \end{bmatrix}$

$\vec{y}=V\vec{p}\ \ \ \ \ \Rightarrow\ \ \ \ \ \vec{p}=(V^TV)^{-1}V^T\vec{y}$

See also: https://en.wikipedia.org/wiki/Polynomial_regression

Functions

Detailed Description

Function Documentation

◆ jkqtpstatPolyFit()