Collaboration diagram for Linear Algebra Tools:

Macros
#define	jkqtplinalgMatIndex(l, c, C) ((l)*(C)+(c))
	calculate the index of the entry in line l and column c in a row-major matrix with C columns

Functions
template<class T >
T	jkqtplinalgDotProduct (const T vec1, const T vec2, long N)
	dot-product between two vectors vec1 and vec2, each with a length of N entries

template<class T >
bool	jkqtplinalgGaussJordan (T *m, long L, long C)
	performs a Gauss-Jordan eliminaion on a LxC matrix m

template<class T >
bool	jkqtplinalgLinSolve (const T A, const T B, long N, long C, T *result_out)
	solve a system of N linear equations $A\cdot\vec{x}=B$ simultaneously for C columns in B

template<class T >
bool	jkqtplinalgLinSolve (const T A, const T b, long N, T *result_out)
	solve a system of N linear equations $A\cdot\vec{x}=\vec{b}$

template<class T >
bool	jkqtplinalgLinSolve (const T A, T b, long N)
	solve a system of N linear equations $A\cdot\vec{x}=\vec{b}$

template<class T >
bool	jkqtplinalgLinSolve (const T A, T B, long N, long C)
	solve a system of N linear equations $A\cdot\vec{x}=B$ simultaneously for C columns in B

template<class T >
T	jkqtplinalgMatrixDeterminant (const T *a, long N)
	determinant the given NxN matrix

template<class T >
bool	jkqtplinalgMatrixInversion (const T matrix, T matrix_out, long N)
	invert the given NxN matrix using Gauss-Jordan elimination

template<class T >
bool	jkqtplinalgMatrixInversion (T *matrix, long N)
	invert the given NxN matrix using Gauss-Jordan elimination

template<class T >
void	jkqtplinalgMatrixProduct (const T M1, const T M2, long N, T *M)
	matrix-matrix product of two NxN matrices

template<class T >
void	jkqtplinalgMatrixProduct (const T M1, long L1, long C1, const T M2, long L2, long C2, T *M)
	matrix-matrix product

template<class T >
void	jkqtplinalgMatrixSwapLines (T *m, long l1, long l2, long C)
	swap two lines in a matrix

template<class T >
std::string	jkqtplinalgMatrixToHTMLString (T matrix, long L, long C, int width=9, int precision=3, const std::string &mode=std::string("g"), const std::string &tableformat=std::string(), const std::string &prenumber=std::string(), const std::string &postnumber=std::string(), bool colorcoding=false, bool zeroIsWhite=true, std::string colorlabel=nullptr, bool nonlinColors=false, double nonlinColorsGamma=0.25, const std::string &colortableformat=std::string())
	convert the given LxC matrix to std::string, encoded as HTML table

template<class T >
std::string	jkqtplinalgMatrixToString (T *matrix, long L, long C, int width=9, int precision=3, const std::string &mode=std::string("g"))
	convert the given LxC matrix to std::string

void	jkqtplinalgPM1ToNonlinRWBColors (double val, uint8_t &r, uint8_t &g, uint8_t &b, double gamma=0.5)
	maps the number range -1 ... +1 to a non-linear color-scale lightblue - white - lightred (used for coloring matrices!)

void	jkqtplinalgPM1ToRWBColors (double val, uint8_t &r, uint8_t &g, uint8_t &b)
	maps the number range -1 ... +1 to a color-scale lightblue - white - lightred (used for coloring matrices!)

template<class T >
void	jkqtplinalgPrintMatrix (const T *matrix, long L, long C, int width=9, int precision=3, char mode='f')
	print the given LxC matrix to std::cout

template<class T >
void	jkqtplinalgTransposeMatrix (T *matrix, long L, long C)
	transpose the given LxC matrix

template<class T >
void	jkqtplinalgTransposeMatrix (T *matrix, long N)
	transpose the given NxN matrix

Detailed Description

This group assembles a basic set of linear algebra methods, including matrix inversion, which are required e.g. by the statistics library (Statistical Computations )

Macro Definition Documentation

◆ jkqtplinalgMatIndex

#define jkqtplinalgMatIndex	(	l,
		c,
		C
	)	((l)*(C)+(c))

calculate the index of the entry in line l and column c in a row-major matrix with C columns

You can use this to access a matrix with L rows and C columns:

for (long l=0; l<L; l++) {
  for (long c=0; c<C; c++) {
    matrix[jkqtplinalgMatIndex(l,c,C)=0;
    if (l==c) matrix[jkqtplinalgMatIndex(l,c,C)=1;
  }
}

Function Documentation

◆ jkqtplinalgDotProduct()

template<class T >

T jkqtplinalgDotProduct	(	const T *	vec1,
		const T *	vec2,
		long	N
	)

inline

dot-product between two vectors vec1 and vec2, each with a length of N entries

Template Parameters

T	of the vector cells (typically double or float)

Parameters

vec1	first vector
vec2	second vector
N	number of entries in vec1 and vec2

◆ jkqtplinalgGaussJordan()

template<class T >

bool jkqtplinalgGaussJordan	(	T *	m,
		long	L,
		long	C
	)

inline

performs a Gauss-Jordan eliminaion on a LxC matrix m

For a matrix equation

$A\cdot\vec{x}=\vec{b}$

the input matrix is

$\left[A | \vec{b}\right]$

for matrix inversion it is

$\left[A | I_L\right]$

where is the unit matrix with LxL entries.

Template Parameters

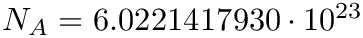
T	of the matrix cells (typically double or float)

Parameters

m	the matrix
L	number of rows in the matrix
C	number of columns in the matrix

See also: http://www.virtual-maxim.de/matrix-invertieren-in-c-plus-plus/

◆ jkqtplinalgLinSolve() [1/4]

template<class T >

bool jkqtplinalgLinSolve	(	const T *	A,
		const T *	B,
		long	N,
		long	C,
		T *	result_out
	)

inline

solve a system of N linear equations 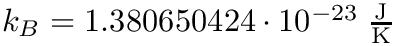$A\cdot\vec{x}=B$ simultaneously for C columns in B

Parameters

A	an NxN matrix of coefficients
B	an NxC marix
N	number of equations
C	number of columns in B
result_out	a NxC matrix with the results after the inversion of the system of equations

Returns: true on success

Note: This function uses the Gauss-Jordan algorithm; It is save to call jkqtpstatLinSolve(A,B,N,C,B) with the same argument for B and result_out. Then the input will be overwritten with the new matrix!

◆ jkqtplinalgLinSolve() [2/4]

template<class T >

bool jkqtplinalgLinSolve	(	const T *	A,
		const T *	b,
		long	N,
		T *	result_out
	)

inline

solve a system of N linear equations 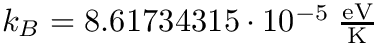$A\cdot\vec{x}=\vec{b}$

Parameters

	A	an NxN matrix of coefficients
	b	an N-entry vector
	N	number of rows and columns in A
[out]	result_out	a N-entry vector with the result

Returns: true on success

Note: This function uses the Gauss-Jordan algorithm; It is save to call jkqtpstatLinSolve(A,B,N,C,B) with the same argument for B and result_out. Then the input will be overwritten with the new matrix!

◆ jkqtplinalgLinSolve() [3/4]

template<class T >

bool jkqtplinalgLinSolve	(	const T *	A,
		T *	b,
		long	N
	)

inline

solve a system of N linear equations 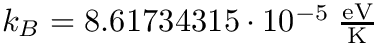$A\cdot\vec{x}=\vec{b}$

Parameters

	A	an NxN matrix of coefficients
[in,out]	b	an N-entry vector (also receives the result)
	N	number of rows and columns in A

Returns: true on success

Note: This function uses the Gauss-Jordan algorithm; It is save to call jkqtpstatLinSolve(A,B,N,C,B) with the same argument for B and result_out. Then the input will be overwritten with the new matrix!

◆ jkqtplinalgLinSolve() [4/4]

template<class T >

bool jkqtplinalgLinSolve	(	const T *	A,
		T *	B,
		long	N,
		long	C
	)

inline

solve a system of N linear equations $A\cdot\vec{x}=B$ simultaneously for C columns in B

Parameters

	A	an NxN matrix of coefficients
[in,out]	B	an NxC marix (also receives the result)
	N	number of equations
	C	number of columns in B

Returns: true on success

Note: This function uses the Gauss-Jordan algorithm; It is save to call jkqtpstatLinSolve(A,B,N,C,B) with the same argument for B and result_out. Then the input will be overwritten with the new matrix!

◆ jkqtplinalgMatrixDeterminant()

template<class T >

T jkqtplinalgMatrixDeterminant	(	const T *	a,
		long	N
	)

inline

determinant the given NxN matrix

Template Parameters

T	of the matrix cells (typically double or float)

Parameters

a	the matrix for which to calculate the determinant
N	number of rows and columns in the matrix

Returns: the determinant of a

Note: for large matrices this algorithm is very slow, think about defining the macro JKQTP_STATISTICS_TOOLS_MAY_USE_EIGEN3 to use faster methods from the EIGEN library!

◆ jkqtplinalgMatrixInversion() [1/2]

template<class T >

bool jkqtplinalgMatrixInversion	(	const T *	matrix,
		T *	matrix_out,
		long	N
	)

inline

invert the given NxN matrix using Gauss-Jordan elimination

Template Parameters

T	of the matrix cells (typically double or float)

Parameters

	matrix	the matrix to invert
[out]	matrix_out	target for the inverted matrix
	N	number of rows and columns in the matrix

Returns: true on success and the inverted matrix in matrix_out.

Note: It is save to call jkqtpstatMatrixInversion(A,A,N) with the same argument for in and out matrix. Then the input will be overwritten with the new matrix!; matrix and matrix_out have to be of size N*N. Matrices are interpreted as row-major!

See also: http://www.virtual-maxim.de/matrix-invertieren-in-c-plus-plus/

◆ jkqtplinalgMatrixInversion() [2/2]

template<class T >

bool jkqtplinalgMatrixInversion	(	T *	matrix,
		long	N
	)

inline

invert the given NxN matrix using Gauss-Jordan elimination

Template Parameters

T	of the matrix cells (typically double or float)

Parameters

[in,out]	matrix	the matrix to invert (at the same time the target)
	N	number of rows and columns in the matrix

◆ jkqtplinalgMatrixProduct() [1/2]

template<class T >

void jkqtplinalgMatrixProduct	(	const T *	M1,
		const T *	M2,
		long	N,
		T *	M
	)

inline

matrix-matrix product of two NxN matrices

Parameters

	M1	matrix 1, size: NxN
	M2	matrix 1, size: NxN
	N	number os rows/columns in the matrices M1, M2 and M
[out]	M	output matrix M=M1*M2, size: NxN

◆ jkqtplinalgMatrixProduct() [2/2]

template<class T >

void jkqtplinalgMatrixProduct	(	const T *	M1,
		long	L1,
		long	C1,
		const T *	M2,
		long	L2,
		long	C2,
		T *	M
	)

inline

matrix-matrix product

Template Parameters

T	of the matrix cells (typically double or float)

Parameters

	M1	matrix 1, size: L1xC1
	L1	number of rows in the matrix M1
	C1	number of columns in the matrix M1
	M2	matrix 1, size: L2xC2
	L2	number of rows in the matrix M2
	C2	number of columns in the matrix M2
[out]	M	output matrix M=M1*M2, size: L1xC2

◆ jkqtplinalgMatrixSwapLines()

template<class T >

void jkqtplinalgMatrixSwapLines	(	T *	m,
		long	l1,
		long	l2,
		long	C
	)

inline

swap two lines in a matrix

Template Parameters

T	of the matrix cells (typically double or float)

Parameters

m	the matrix to work on
l1	the row to swap with row l2
l2	the row to swap with row l1
C	number of columns in the matrix

◆ jkqtplinalgMatrixToHTMLString()

template<class T >

std::string jkqtplinalgMatrixToHTMLString	(	T *	matrix,
		long	L,
		long	C,
		int	width = `9`,
		int	precision = `3`,
		const std::string &	mode = `std::string("g")`,
		const std::string &	tableformat = `std::string()`,
		const std::string &	prenumber = `std::string()`,
		const std::string &	postnumber = `std::string()`,
		bool	colorcoding = `false`,
		bool	zeroIsWhite = `true`,
		std::string *	colorlabel = `nullptr`,
		bool	nonlinColors = `false`,
		double	nonlinColorsGamma = `0.25`,
		const std::string &	colortableformat = `std::string()`
	)

inline

convert the given LxC matrix to std::string, encoded as HTML table

Template Parameters

type	of the matrix cells (typically double or float)

Parameters

	matrix	the matrix to convert
	L	number of lines/rows in the matrix
	C	number of columns in the matrix
	width	width (in characters) of each cell in the output (used for formatting)
	precision	precision (in digits) for string-conversions in the output (used for formatting)
	mode	the (printf()) string conversion mode for output of the cell values
	tableformat	this is inserted into the `<table`...> tag (may contain HTML property definitions)
	prenumber	this is inserted before each number (may contain HTML markup)
	postnumber	this is inserted after each number (may contain HTML markup)
	colorcoding	if `true`, teh cell backgrounds are color-coded
	zeroIsWhite	if `the` color-coding is forced to white for 0 and then encodes in positive/negative direction with colors (red and blue)
[out]	colorlabel	outputs a label explaining the auto-generated color-coding
	nonlinColors	if `true`, a non-linear color-coding is used
	nonlinColorsGamma	gamma-value for a non-linear color-coding
	colortableformat	lie tableformat, but for the legend table output in colorLabel

See also: jkqtplinalgPM1ToNonlinRWBColors() and jkqtplinalgPM1ToRWBColors()

◆ jkqtplinalgMatrixToString()

template<class T >

std::string jkqtplinalgMatrixToString	(	T *	matrix,
		long	L,
		long	C,
		int	width = `9`,
		int	precision = `3`,
		const std::string &	mode = `std::string("g")`
	)

inline

convert the given LxC matrix to std::string

Template Parameters

type	of the matrix cells (typically double or float)

Parameters

matrix	the matrix to convert
L	number of lines/rows in the matrix
C	number of columns in the matrix
width	width (in characters) of each cell in the output (used for formatting)
precision	precision (in digits) for string-conversions in the output (used for formatting)
mode	the (printf()) string conversion mode for output of the cell values

◆ jkqtplinalgPM1ToNonlinRWBColors()

void jkqtplinalgPM1ToNonlinRWBColors	(	double	val,
		uint8_t &	r,
		uint8_t &	g,
		uint8_t &	b,
		double	gamma = `0.5`
	)

inline

maps the number range -1 ... +1 to a non-linear color-scale lightblue - white - lightred (used for coloring matrices!)

Parameters

	val	the value to convert
[out]	r	returns the red value (0..255)
[out]	g	returns the green value (0..255)
[out]	b	returns the blue value (0..255)
	gamma	a gamma-value for non-linear color scaling

◆ jkqtplinalgPM1ToRWBColors()

void jkqtplinalgPM1ToRWBColors	(	double	val,
		uint8_t &	r,
		uint8_t &	g,
		uint8_t &	b
	)

inline

maps the number range -1 ... +1 to a color-scale lightblue - white - lightred (used for coloring matrices!)

Parameters

	val	the value to convert
[out]	r	returns the red value (0..255)
[out]	g	returns the green value (0..255)
[out]	b	returns the blue value (0..255)

◆ jkqtplinalgPrintMatrix()

template<class T >

void jkqtplinalgPrintMatrix	(	const T *	matrix,
		long	L,
		long	C,
		int	width = `9`,
		int	precision = `3`,
		char	mode = `'f'`
	)

inline

print the given LxC matrix to std::cout

Template Parameters

type	of the matrix cells (typically double or float)

Parameters

matrix	the matrix to print out
L	number of lines/rows in the matrix
C	number of columns in the matrix
width	width (in characters) of each cell in the output (used for formatting)
precision	precision (in digits) for string-conversions in the output (used for formatting)
mode	if `=='f'` the mode `std::fixed` is used for output, otherwise `std::scientific` is used

◆ jkqtplinalgTransposeMatrix() [1/2]

template<class T >

void jkqtplinalgTransposeMatrix	(	T *	matrix,
		long	L,
		long	C
	)

inline

transpose the given LxC matrix

Template Parameters

T	of the matrix cells (typically double or float)

Parameters

matrix	the matrix to transpose
L	number of rows in the matrix
C	number of columns in the matrix

Note: The output is interpreted as CxL matrix!!!

◆ jkqtplinalgTransposeMatrix() [2/2]

template<class T >

void jkqtplinalgTransposeMatrix	(	T *	matrix,
		long	N
	)

inline

transpose the given NxN matrix

Template Parameters

T	of the matrix cells (typically double or float)

Parameters

matrix	the matrix to transpose
N	number of rows and columns in the matrix

Macros

Functions

Detailed Description

Macro Definition Documentation

◆ jkqtplinalgMatIndex

Function Documentation

◆ jkqtplinalgDotProduct()

◆ jkqtplinalgGaussJordan()

◆ jkqtplinalgLinSolve() [1/4]

◆ jkqtplinalgLinSolve() [2/4]

◆ jkqtplinalgLinSolve() [3/4]

◆ jkqtplinalgLinSolve() [4/4]

◆ jkqtplinalgMatrixDeterminant()

◆ jkqtplinalgMatrixInversion() [1/2]

◆ jkqtplinalgMatrixInversion() [2/2]

◆ jkqtplinalgMatrixProduct() [1/2]

◆ jkqtplinalgMatrixProduct() [2/2]

◆ jkqtplinalgMatrixSwapLines()

◆ jkqtplinalgMatrixToHTMLString()

◆ jkqtplinalgMatrixToString()

◆ jkqtplinalgPM1ToNonlinRWBColors()

◆ jkqtplinalgPM1ToRWBColors()

◆ jkqtplinalgPrintMatrix()

◆ jkqtplinalgTransposeMatrix() [1/2]

◆ jkqtplinalgTransposeMatrix() [2/2]