Example (JKQTPlotter): Plotting Parsed Mathematical Functions as Line Graphs

Plot Function f(x)

This project (see ./examples/parsedfunctionplot/) demonstrates how to plot mathematical functions as line graphs. The functions are defined as strings that will be evaluated with the equation parser, integrated into JKQTPlotter.

Note: See the example Plotting Mathematical Functions as Line Graphs if you don't want to draw parsed functions, but want to provide a C function, or C++ functor!

Adding an evaluated funtion to a graph is very simple:

JKQTPXParsedFunctionLineGraph* parsedFunc=new JKQTPXParsedFunctionLineGraph(plot);
parsedFunc->setFunction("sin(x*8)*exp(-x/4)");
parsedFunc->setTitle("user function");

As you can see a graph of the type JKQTPXParsedFunctionLineGraph is used, which plots a function that depends on the variable x. The given function is parsed and evaluated (see lib/jkqtcommon/jkqtpmathparser.h for details on the features of the math parser). An intelligent drawing algorithm chooses the number of control points for drawing a smooth graph, with sufficient amount of details, by evaluating locally the slope of the function.

In the example in examples/parsedfunctionplot/parsedfunctionplot.cpp we do not simply set a fixed function, but add a QLineEdit which allows to edit the function and redraws it, once ENTER is pressed:

JKQTPlotter* plot=new JKQTPlotter(&mainWin);
QLineEdit* edit=new QLineEdit(&mainWin);
edit->setToolTip("enter a function in dependence of the variable <tt>x</tt> and press ENTER to update the graph");
 
// ...
 
 
// 2. now we add a JKQTPXParsedFunctionLineGraph object, which will draw the function from
//    the line edit
JKQTPXParsedFunctionLineGraph* parsedFunc=new JKQTPXParsedFunctionLineGraph(plot);
plot->addGraph(parsedFunc);
//    finally we connect the line edit with the graph, whenever RETURN is pressed,
//    the graph is updated:
auto updateGraphFunctor=
   [=]() {
    parsedFunc->setTitle("user function: \\verb{"+edit->text()+"}");
    parsedFunc->setFunction(edit->text());
    plot->redrawPlot();
   };
QObject::connect(edit, &QLineEdit::returnPressed, updateGraphFunctor);
QObject::connect(edit, &QLineEdit::editingFinished, updateGraphFunctor);
edit->setText("sin(x*8)*exp(-x/4)");
updateGraphFunctor();

This code snippet results in a plot like this:

Plotting with parameters

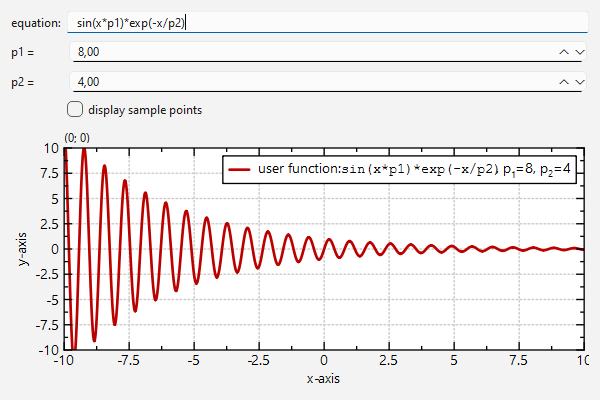
As shown in Plotting Mathematical Functions as Line Graphs you can also use externally set parameters in a plot function. These parameters can be double numbers and may be set with either as an internal parameter vector, or may be read from a parameter column (as shown in the linked example). These parameters are available as variables p1, p2, ... in the function string. Here is a small example:

JKQTPXParsedFunctionLineGraph* parsedFunc=new JKQTPXParsedFunctionLineGraph(plot);
parsedFunc->setFunction("sin(x*p1)*exp(-x/p2)");
parsedFunc->setParamV(/*p1=*/8, /*p2=*/4);
parsedFunc->setTitle("user function");

Plot Function f(y)

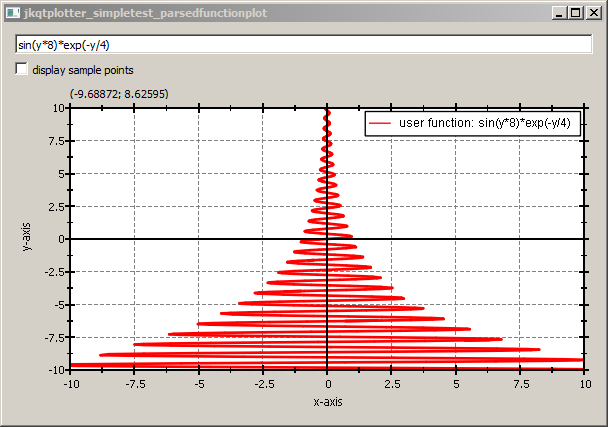
If you use the graph class JKQTPYParsedFunctionLineGraph instead of JKQTPXParsedFunctionLineGraph, you can plot functions x=f(y) (instead of y=f(x)). The function from the example above will then ahve to be changed to sin(y*8)*exp(-y/4) and the result will look like this:

Properties of the Adaptive Plotting Algorithm

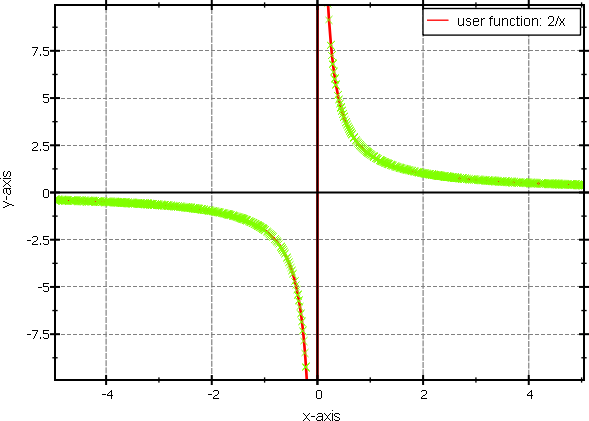
The adaptive capabilities of the rendering algorithm can be seen, when plotting e.g. 2/x, which is drawn smoothely, even around the undefined value at x=0:

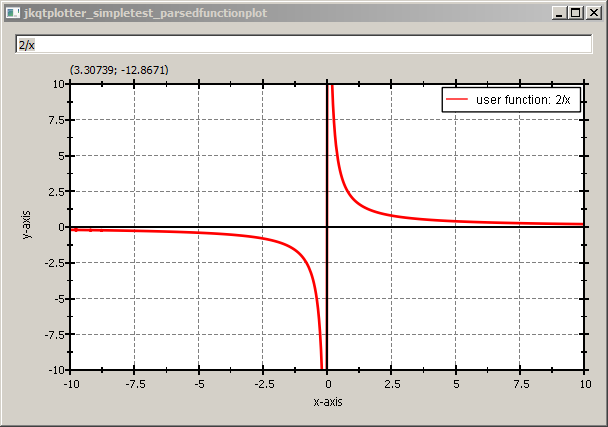
With an additional checkbox in this example, you can switch drawing the actual sample points of the drawing algorithm on and off, by calling parsedFunc->setDisplaySamplePoints(...). This can be used to debug the drawing algorithm and explore its parameters (which you can set with setMinSamples(), setMaxRefinementDegree(), setSlopeTolerance(), setMinPixelPerSample()). Here is an example of a 2/x function with shown sample points: